Hypercycle (geometry)
In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.
Given a straight line L and a point P not on L, we can construct a hypercycle by taking all points Q on the same side of L as P, with perpendicular distance to L equal to that of P.
The line L is called the axis, center, or base line of the hypercycle. The orthogonal segments from each point to L are called radii. Their common length is called distance.
In the Poincaré disk and half-plane models of the hyperbolic plane, hypercycles are represented by lines and circles arcs that intersect the boundary circle/line at non-right angles. The representation of the axis intersects the boundary circle/line in the same points, but at right angles.
The hypercycles through a given point that share a tangent through that point converge towards a horocycle as their distances go towards infinity.
Hypercycles in hyperbolic geometry have some properties similar to those of circles in Euclidean geometry:
- A line perpendicular to a chord of a hypercycle at its midpoint is a radius and it bisects the arc subtended by the chord.
Let AB be the chord and M its middle point. By symmetry the line R through M perpendicular to AB must be orthogonal to the axis L. Therefore R is a radius. Also by symmetry, R will bisect the arc AB.
- The axis and distance of an hypercycle is uniquely determined.
Let us assume that a hypercycle C has two different axes 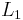 and
and 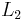 . Using the previous property twice with different chords we can determine two distinct radii
. Using the previous property twice with different chords we can determine two distinct radii 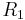 and
and 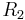 .
. 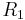 and
and 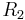 will then have to be perpendicular to both
will then have to be perpendicular to both 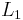 and
and 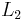 , giving us a rectangle. This is a contradiction because the rectangle is an impossible figure in hyperbolic geometry.
, giving us a rectangle. This is a contradiction because the rectangle is an impossible figure in hyperbolic geometry.
- Two hypercycles have equal distances Iff they are congruent.
If they have equal distance, we just need to bring the axes to coincide by a rigid motion and also all the radii will coincide; since the distance is the same, also the points of the two hypercycles will coincide. Vice versa, if they are congruent the distance must be the same by the previous property.
- A straight line cuts a hypercycle in at most two points.
Let the line K cut the hypercycle C in two points A and B. As before, we can construct the radius R of C through the middle point M of AB. Note that K is ultraparallel to the axis L because the have the common perpendicular R. Also, two ultraparallel lines have minimum distance at the common perpendicular and monotonically increasing distances as we go away from the perpendicular. This means that the points of K inside AB will have distance from L smaller than the common distance of A and B from L, while the points of K outside AB will have greater distance. In conclusion, no other point of K can be on C.
- Two hypercycles intersect in at most two points.
Let 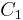 and
and 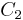 be hypercycles intersecting in three points A, B, and C. If
be hypercycles intersecting in three points A, B, and C. If 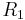 is the line orthogonal to AB through its middle point, we know that it is a radius of both
is the line orthogonal to AB through its middle point, we know that it is a radius of both 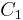 and
and 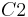 . Similarly we construct
. Similarly we construct 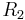 , the radius through the middle point of BC.
, the radius through the middle point of BC. 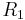 and
and 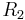 are simultaneously orthogonal to the axes
are simultaneously orthogonal to the axes 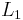 and
and 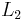 of
of 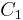 and
and 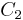 , respectively. We already proved that then
, respectively. We already proved that then 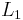 and
and 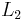 must coincide (otherwise we have a rectangle). Then
must coincide (otherwise we have a rectangle). Then 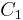 and
and 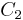 have the same axis and at least one common point, therefore they have the same distance and they coincide.
have the same axis and at least one common point, therefore they have the same distance and they coincide.
- No three points of a hypercycle are collinear.
If the points A, B, and C of an hypercycle are collinear then the chords AB and BC are on the same line K. Let 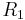 and
and 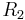 be the radii through the middle points of AB and BC. We know that the axis L of the hypercycle is the common perpendicular of
be the radii through the middle points of AB and BC. We know that the axis L of the hypercycle is the common perpendicular of 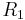 and
and 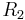 . But K is that common perpendicular.
. But K is that common perpendicular.
Then the distance must be 0 and the hypercycle degenerates into a line.
References
- Martin Gardner, Non-Euclidean Geometry, Chapter 4 of The Colossal Book of Mathematics, W. W. Norton & Company, 2001, ISBN 978-0-393-02023-6
- M. J. Greenberg, Euclidean and Non-Euclidean Geometries: Development and History, 3rd edition, W. H. Freeman, 1994.
- George E. Martin, The Foundations of Geometry and the Non-Euclidean Plane, Springer-Verlag, 1975.
- David C. Royster, Neutral and Non-Euclidean Geometries.